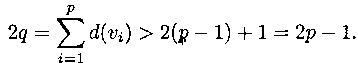[Список тем]
[Вступление к этой теме]
[1]
[2]
[3]
Деревья
1. Определения
Определение |
Граф без циклов называется ациклическим, или лесом. Связный ациклический граф
называется (свободным) деревом. Таким образом, компонентами связности леса
являются деревья.
|
ЗАМЕЧАНИЕ |
Прилагательное "свободное" употребляется в том случае, когда нужно
подчеркнуть отличие деревьев от других объектов, родственных деревьям:
ориентированных деревьев, упорядоченных деревьев и т. д.
|
В связном графе G выполняется неравенство q(G)>= p(G) - 1.
Граф G, в котором q(G)=p(G)-1, называется древовидным.
В ациклическом графе G z(G) = 0. Пусть u, v - несмежные
вершины графа G, х=(u, v)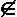 Е.
Если граф G + х имеет только один простой цикл, z(G + х) = 1,
то граф G называется субциклическим.
Е.
Если граф G + х имеет только один простой цикл, z(G + х) = 1,
то граф G называется субциклическим.
Пример
На рис. 1 показаны диаграммы всех различных (свободных) деревьев с 5
вершинами, а на рис. 2 - диаграммы всех различных (свободных) деревьев
с 6 вершинами.
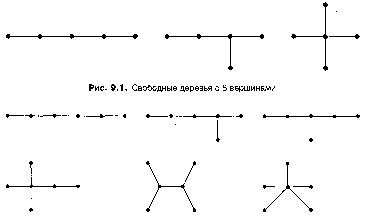
Рис 2. Свободные деревья с 6 вершинами
2. Основные свойства деревьев
Следующая теорема устанавливает, что два из четырех свойств - связность,
ацикличность, древовидность и субцикличность - характеризуют граф
как дерево.
ТЕОРЕМА |
Пусть G(V, Е) - граф с р вершинами, q ребрами,
k компонентами связности и z простыми циклами.
Пусть далее х - ребро, соединяющее любую пару несмежных
вершин в G. Тогда следующие утверждения эквивалентны:
1. G - дерево, то есть связный граф без циклов,
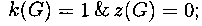
2. любые две вершины соединены в G единственной простой цепью,
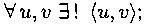
3. G - связный граф, и любое ребро есть мост,
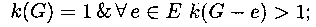
4. G - связный и древовидный,
k(G) = 1 & q(G) = p(G) - 1;
5. G - ациклический и древовидный,
z(G) = 0 & q(G) = p(G) - 1;
6. G - ациклический и субциклический,
z(G) = 0 & z(G+x) = 1;
7. G - связный, субциклический и неполный,
k(G) = 1 & G 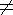 Kр & р>= 3 & z(G + x) = 1;
Kр & р>= 3 & z(G + x) = 1;
8. G - древовидный и субциклический (за двумя исключениями),
q(G) = p(G) - 1 & G 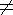 K1 >=
K3 & G
K1 >=
K3 & G 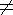 K2 >= К3 & z(С + x) = 1.
K2 >= К3 & z(С + x) = 1.
|
доказательство
1 ==>
2 : От противного. Пусть существуют две цепи <u, v> (рис. 3 слева). Тогда w1, w2 - простой цикл.
2 ==>
3 : Имеем: 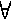 u, v
u, v 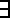 ! <u, v>, следовательно, k(G) = 1. Далее от противного. Пусть ребро x - не мост. Тогда в G - х концы этого ребра связаны цепью. Само ребро х - вторая цепь.
! <u, v>, следовательно, k(G) = 1. Далее от противного. Пусть ребро x - не мост. Тогда в G - х концы этого ребра связаны цепью. Само ребро х - вторая цепь.
3 ==>
4 : Индукция по р. База: р = 1 ==>
q = 0. Пусть q(G) = p(G) -1 для всех графов G с числом вершин меньше р. Тогда удалим из G ребро х (которое является мостом). Получим две компоненты G' и G", удовлетворяющие индукционному предположению. Имеем:
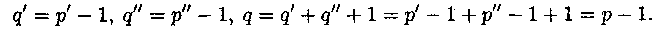
4 ==>
5 : От противного. Пусть есть цикл с n вершинами и n ребрами. Остальные р - n вершин имеют инцидентные им ребра, которые связывают их с циклом. Следовательно, q> = р, что противоречит условию q = р - 1.
5 ==>
1 : Граф без циклов, следовательно, его компоненты - деревья. Пусть их k. Имеем:
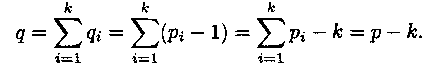
Но q = р - 1, следовательно, k = 1.
5 ==>
6 : По ранее доказанному 5 ==>
1 ==>
2. Имеем: 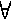 u, v
u, v 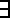 ! <u, v>. Соединив две несмежные вершины, получим
единственный простой цикл.
! <u, v>. Соединив две несмежные вершины, получим
единственный простой цикл.
6 ==>
7: При р >=
3 граф Кр содержит цикл, следовательно,
G 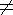 Kр. Далее от противного. Пусть G несвязен, тогда при
соединении ребром двух компонент связности цикл не возникнет.
Kр. Далее от противного. Пусть G несвязен, тогда при
соединении ребром двух компонент связности цикл не возникнет.
7 ==>
2 : Имеем k(G) = 1, следовательно,  u, v
u, v 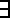 <u, v>. Пусть цепь не единственная. Тогда существует
цикл Z, причем Z = К3 = С3.
Действительно, пусть Z > С3, тогда, соединив
две несмежные вершины этого цикла, получим два цикла. Но G
связен и G
<u, v>. Пусть цепь не единственная. Тогда существует
цикл Z, причем Z = К3 = С3.
Действительно, пусть Z > С3, тогда, соединив
две несмежные вершины этого цикла, получим два цикла. Но G
связен и G 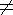 К3, следовательно, существует другая вершина w,
смежная с Z = К3 (рис. 3 справа). Если w смежна
с более чем одной вершиной Z, то имеем больше одного цикла,
Если w смежна только с одной вершиной Z, то соединив ее
с другой вершиной, получим два цикла.
К3, следовательно, существует другая вершина w,
смежная с Z = К3 (рис. 3 справа). Если w смежна
с более чем одной вершиной Z, то имеем больше одного цикла,
Если w смежна только с одной вершиной Z, то соединив ее
с другой вершиной, получим два цикла.
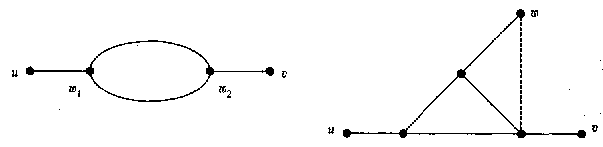
Рис. 3. Иллюстрации к доказательству теоремы о свойствах деревьев
7 ==> 8 : Имеем k(G) = 1, следовательно,
G 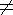 К2 U К3,
G
К2 U К3,
G 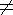 К1 U К3.
Имеем по доказанному: 7 ==> 2 ==> 3 ==> 4, то есть
q = р - 1.
К1 U К3.
Имеем по доказанному: 7 ==> 2 ==> 3 ==> 4, то есть
q = р - 1.
8 ==>
5 : От противного. Пусть в G есть цикл Z = Сn.
Если n > 3, то если внутри Z уже есть смежные вершины,
имеем два цикла. Если в Z нет смежных вершин, то, соединив несмежные
вершины в Z, получим два цикла. Следовательно,
Z = К3. Этот цикл Z является компонентой
связности G. Действительно, пусть это не так. Тогда
существует вершина w, смежная с Z. Если w
смежна более чем с одной вершиной Z, то имеем больше одного цикла.
Если w смежна только с одной вершиной Z, то, соединив ее с
другой вершиной, получим два цикла. Рассмотрим G': = G - Z. Имеем:
р = р' + 3, q = q' + 3. Но q = р -1, следовательно,
q' = р' -1. Отсюда z(G') = 0, так как один цикл уже есть.
Следовательно, компоненты G' - деревья. Пусть их k. Имеем:
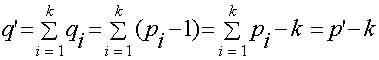
но q' = р' - 1, следовательно, k = 1, то есть дерево одно.
Если в этом дереве соединить несмежные вершины, то получим второй цикл.
Два исключения: деревья, которые не имеют несмежных вершин, - это
K1 и К2.
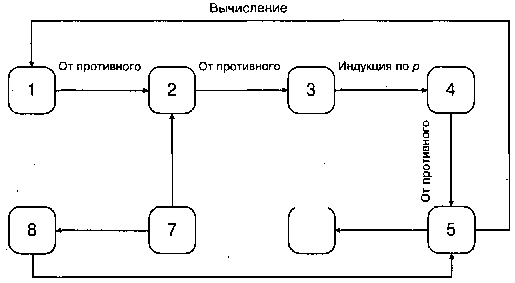
Общая схема доказательства представлена на рис. 4. Граф доказательства
сильно связен, следовательно, теорема доказана.
СЛЕДСТВИЕ |
В любом нетривиальном дереве имеются по крайней мере две висячие вершины.
|
доказательство
Рассмотрим дерево С(V, Е). Дерево - связный граф, следовательно,
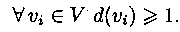
От противного
Рис. 4. Схема доказательства теоремы о свойствах деревьев
Далее от противного. Пусть 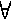 vi
vi 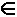 1..р - 1 d(v) > 1. Тогда
1..р - 1 d(v) > 1. Тогда
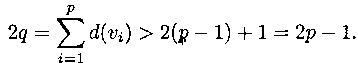
Но q = p - 1, то есть 2q = 2р - 2. Имеем противоречие: 2р - 2 > 2р - 1.
[Список тем]
[Вступление к этой теме]
[1]
[2]
[3]
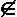 Е.
Если граф G + х имеет только один простой цикл, z(G + х) = 1,
то граф G называется субциклическим.
Е.
Если граф G + х имеет только один простой цикл, z(G + х) = 1,
то граф G называется субциклическим.
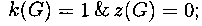
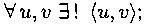
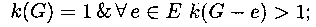
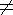 Kр & р>= 3 & z(G + x) = 1;
Kр & р>= 3 & z(G + x) = 1;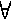 u, v
u, v 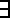 ! <u, v>, следовательно, k(G) = 1. Далее от противного. Пусть ребро x - не мост. Тогда в G - х концы этого ребра связаны цепью. Само ребро х - вторая цепь.
! <u, v>, следовательно, k(G) = 1. Далее от противного. Пусть ребро x - не мост. Тогда в G - х концы этого ребра связаны цепью. Само ребро х - вторая цепь.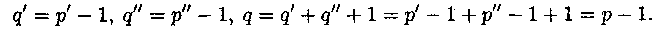
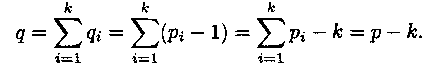

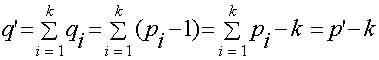
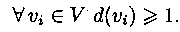

 1..р - 1 d(v) > 1. Тогда
1..р - 1 d(v) > 1. Тогда