| Столбцы |
Пояснения |
| 1,2 |
В первую очередь в скобках выполняется
отрицание. Находим инверсии. |
| 3 |
Конъюнкция - операция сохраняющая 0, т.е. если  b=0
или b=0
или  c=0, то результат 0 c=0, то результат 0 |
| 4 |
Импликация ложна тогда и только тогда, когда
посылка (a)-истинна, а заключение - ложно. |
| 5,6 |
Находим инверсии a и d, которые надо
выполнить раньше дизъюнкции. |
| 7 |
Дизъюнкция - операция сохраняющая 1, т.е. если  a=1
или a=1
или  d=1, то результат 1. d=1, то результат 1. |
| 8 |
Равнозначность истинна, если в 4 и 7 столбцах
одинаковые значения и ложна, если разные. |
Результат последнего действия и есть
логическое значение функции.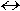 b & c)
b & c) 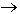 a
a 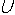
 d)
d)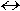 b
b 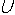 c)
c) 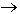 a &
a & d)
d)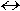
 b &
b &  c)
c) 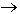
 a
a 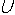 d)
d)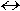
 b
b 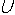
 c)
c)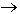
 a &d)
a &d)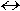 b &
b &  c)
c) 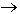
 a
a 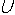
 d)
d)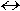 b
b 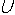
 c)
c) 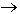
 a &
a & d)
d)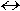
 b & c)
b & c) 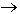 a
a 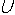 d)
d)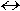
 b
b 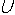 c)
c) 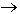 a &d)
a &d) a
a 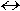 b & c)
b & c) 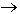
 a
a 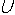
 d)
d) a
a 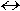 b
b 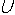 c)
c) 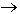
 a &
a & d)
d) a
a 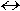
 b &
b &  c)
c) 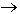 a
a 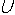 d)
d) a
a 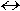
 b
b 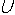
 c)
c) 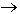 a &d)
a &d) a
a 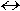 b &
b &  c)
c) 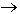 a
a 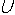
 d)
d) a
a 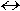 b
b 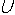
 c)
c) 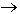 a &
a & d)
d) a
a 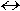
 b & c)
b & c) 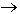 a
a 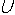
 d)
d) a
a 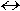
 b
b 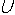 c)
c) 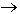 a &
a & d)
d)