[Список тем]
Перевод логического выражения из базиса И-НЕ в базис ИЛИ-НЕ
| Вариант № |
Исходное выражение |
|
Вариант № |
Исходное выражение |
| 1 |
( b|d) | (a| b|d) | (a| b|c) | ( b|c) | ( a| a| b| b| c) c) |
|
9 |
 b | (a | b | (a | c| c| d) | ( d) | ( a|c| a|c| d) d) |
| 2 |
(a|c) | (a|b|d) | (a| b| b| d) d) |
|
10 |
a | (b | c| c| d) | ( d) | ( b| b| c|d) c|d) |
| 3 |
(b|d) | (a|b| c) | ( c) | ( a|b|c) a|b|c) |
|
11 |
b | (a |c| d) | ( d) | ( a| a| c| c| d) d) |
| 4 |
( a|c)
| ( a|c)
| ( a|b| a|b| d) | ( d) | ( a| a| b|d) b|d)
|
|
12 |
 a |
(b | a |
(b | c|d) | ( c|d) | ( b| b| c| c| d) d) |
| 5 |
( a| a| b) | ( b) | ( b|c|d) | ( b|c|d) | ( b| b| c| c| d) d) |
|
13 |
 b |
(a |c| b |
(a |c| d) | (a| d) | (a| c|d) c|d) |
| 6 |
(a| b)
| (a| b)
| (a| c| c| d) | (a|c|d) d) | (a|c|d) |
|
14 |
a | (b | c|d) | (b|c| c|d) | (b|c| d) d) |
| 7 |
(a|b) | (b|c|d) | ( b| b| c| c| d) d) |
|
15 |
b | ( a | a | c|d)
| ( c|d)
| ( a|c| a|c| d) d) |
| 8 |
( a|b)
| ( a|b)
| ( a|c|d) | ( a|c|d) | ( a| a| c| c| d) d) |
|
16 |
 a |
( a |
( b | b | c|d) | ( c|d) | ( b|c| b|c| d) d) |
Пример.
Для функции  с | (
с | ( a |
a | b|d) | (a|b|
b|d) | (a|b| d)
последовательно выполним пункты алгоритма.
Получаем MДНФ: с
d)
последовательно выполним пункты алгоритма.
Получаем MДНФ: с 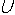 (
( a &
a & b&d)
b&d) 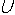 (a&b&
(a&b&
 d)
Одиночный аргумент функции поменял знак.
Заполним карту Вейча из 16 клеток единицами в
соответствии с сочетаниями значений переменных
в элементарных конъюнкциях. Оставшиеся клетки
карты заполняем нулями и охватываем их
замкнутыми прямоугольными областями по 2n
(где n-целое) клеток.
d)
Одиночный аргумент функции поменял знак.
Заполним карту Вейча из 16 клеток единицами в
соответствии с сочетаниями значений переменных
в элементарных конъюнкциях. Оставшиеся клетки
карты заполняем нулями и охватываем их
замкнутыми прямоугольными областями по 2n
(где n-целое) клеток.
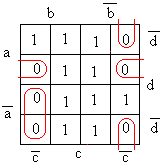
Стремимся, чтобы областей было минимальное
количество, и каждая из них охватывала
максимальное число клеток. Запишем МКНФ,
элементарные дизъюнкции которой составляется из
отрицаний значений аргументов функции, не
меняющих в пределах прямоугольной области свой
знак: (a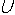
 b
b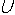 с) & (b
с) & (b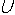 с
с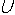 d) & (
d) & ( a
a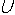 с
с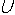
 d). Переходим к базису ИЛИ-НЕ:
d). Переходим к базису ИЛИ-НЕ:
(a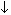
 b
b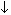 с)
с) 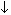 (b
(b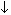 с
с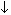 d)
d)
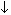 (
( a
a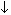 с
с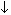
 d).
d).
[Список тем]
 b|d) | (a|
b|d) | (a| b|c) | (
b|c) | ( a|
a| b|
b| c)
c) b | (a |
b | (a | c|
c| d) | (
d) | ( a|c|
a|c| d)
d) b|
b| d) | (
d) | ( b|
b| c|d)
c|d) a|b|c)
a|b|c) a|
a| c|
c| d)
d) a|c)
| (
a|c)
| ( a|b|
a|b| d) | (
d) | ( a|
a| b|d)
b|d)
 a |
(b |
a |
(b | c|d) | (
c|d) | ( b|
b| c|
c| d)
d) a|
a| b) | (
b) | ( b|c|d) | (
b|c|d) | ( b|
b| c|
c| d)
d) b |
(a |c|
b |
(a |c| d) | (a|
d) | (a| c|d)
c|d) b)
| (a|
b)
| (a| c|
c| d) | (a|c|d)
d) | (a|c|d) b|
b| d)
d) c|d)
| (
c|d)
| ( a|c|
a|c| d)
d) a|b)
| (
a|b)
| ( a|c|d) | (
a|c|d) | ( a|
a| c|
c| d)
d) a |
(
a |
( b |
b | c|d) | (
c|d) | ( b|c|
b|c| d)
d) (
(